[개념정리] Linear Algebra

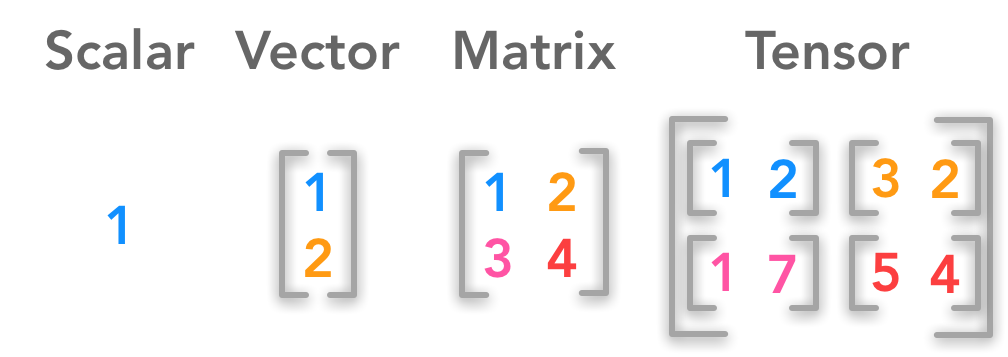
Tensor

텐서는 행과 열로 구성된 2차원 행렬이 아닌 n차원으로 일반화한 행렬이다.

행렬의 덧셈, 뺄셈

행렬의 덧셈, 뺄셈은 각 원소에 대응하는 스칼라 값들을 더하고 빼는 연산을 하면 된다. 이때 각 행과 열에 대응하는 원소들로 연산하기 때문에 행렬에 크기가 서로 같아야 한다.

행렬의 스칼라곱과 행렬곱

스칼라곱은 해당 행렬의 모든 원소에 스칼라를 곱하는 연산이다. 행렬의 각 원소를 스칼라배 하는 것으로 벡터의 크기를 다룰 때 사용할 수 있다.

행렬곱은 행렬간의 곱을 의미한다. 아래 그림과 같이 사이즈가 중요하다.

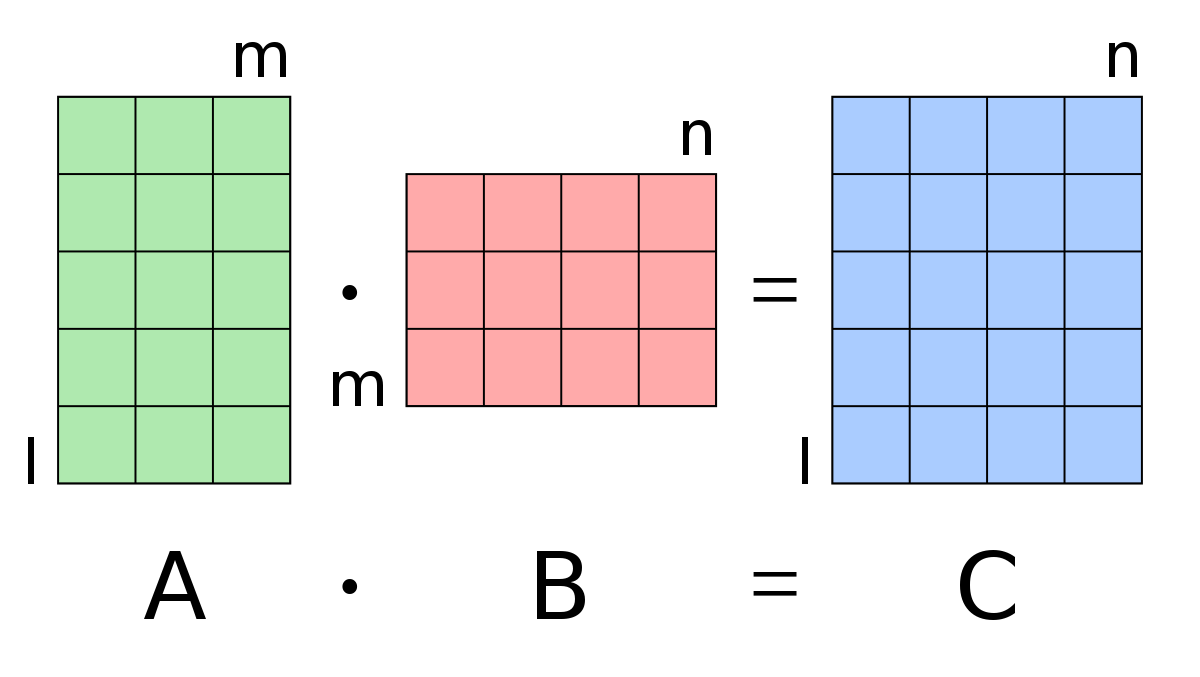
행렬식(Determinant)

행렬식은 행렬의 특성을 하나의 숫자로 표현하는 방법이다. 선형대수에서 행렬식은 정사각행렬에 수를 대응시키는 하나의 함수인데 대략, 정사각행렬이 나타내는 선형 변환이 부피를 확대시키는 정도를 나타낸다. 행렬식의 절댓값은 해당 행렬이 단위 공간을 얼마나 늘렸는지 혹은 줄였는지를 나타내는데 행렬식이 1인 경우 단위 공간의 부피와 같고 10이라면 단위 공간의 10배의에 해당하는 것을 의미한다.

선형 변환

선형 변환은 두 벡터 공간 사이의 함수이다. 예를 들어 좌표 평면에 벡터 하나가 있다고 가정할 때, 그 벡터를 확대하거나 축소하거나 회전하거나 반사하는 것을 모두 변환이라고 생각할 수 있다. 행렬과 벡터의 곱 $Ax$는 벡터 $x$를 선형 변환 $A$를 취한 것을 의미한다. 행렬, 벡터를 다른 좌표 공간으로 이동시킨다고 생각할 수 있다.

벡터 공간과 기저

벡터 공간이란 벡터 집합이 존재할 때, 헤당 벡터들로 구성할 수 있는 공간을 의미한다. 기저(basis)는 이러한 벡터 공간을 생성하는 선형 독립인 벡터들이다. 이때 벡터 공간의 일부를 부분 공간(Subspace)라고 부르는데, 예를 들어, 전체 벡터 공간 V가 3차원이고 2개의 기저 벡터 집합을 S라고 라고 할 때, 부분 공간 W는 2개의 기저 벡터가 span하는 V안의 2차원 평면을 나타낸다.

기저는 Unique하지 않고 여러개 존재할 수 있다. 다만 계산의 편의를 위해 단위 벡터들을 주로 사용한다.

랭크와 차원

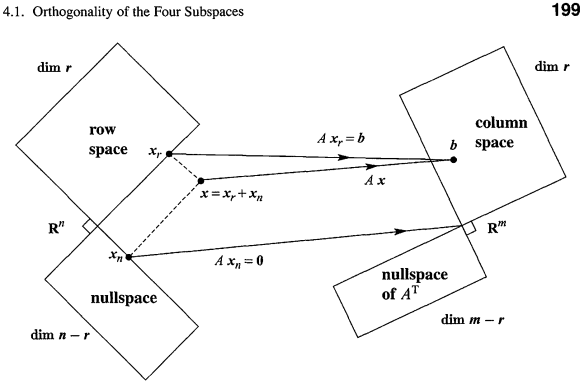
Column vector로 span하는 space를 column space, row vector로 span하는 space를 row space라고 한다. 이때 각 공간의 차원은 각 공간의 기저 벡터의 개수와 같다. 예를 들어, column basis가 3개면 column space는 3차원 공간이 된다. 이러한 차원을 Rank(특히 column space의 차원)이라고 한다. 이때 column space의 rank와 row space의 rank는 같은데 이는 특정 행렬에서 행과 열의 선형 독립인 벡터의 개수가 같다는 것을 의미한다. 또한 영공간(null space)란 행렬 $A$가 주어질 때 $Ax=0$을 만족하는 모든 벡터 $x$의 집합이라고 할 수 있다.

고윳값, 고유 벡터

고윳값, 고유 벡터는 특성값, 특성 벡터라고 생각할 수 있고, 이들은 행렬의 특성을 나타내는 것들이다. 벡터는 방향(direction)과 크기(magnitude)로 결정되는데, 여기서 특성이란 방향은 변하지 않고 크기만 변하는 특성을 말한다. 즉, 고유 벡터란 벡터에 선형 변환을 취했을 때, 방향은 변하지 않고 크기만 변하는 벡터를 의미한다. 그리고 선형 변환 이후 변한 크기가 고윳값을 의미한다.

\[Ax =\lambda x\]

위 식의 의미는 벡터 $x$에 선형 변환 $A$를 취했는데, 그 결과는 기존 벡터의 방향은 변하지 않고 길이가 $\lambda$만큼 변했다는 것을 의미한다. 정리하자면, 고유 벡터란 어떤 벡터에 선형 변환을 취했을 때, 방향은 변하지 않고, 크기만 바뀌는 벡터를 의미하고, 고윳값이란 고유 벡터가 변화되는 ‘크기’의 정도를 의미한다.